This post is also available in: Italiano (Italian)
All wonderful hi-res planetary images currently taken by many amateur astronomers worldwide are all based on the same technique, i.e. selecting and aligning a lot of single frames from a single movie (typically an AVI file), which are then stacked and processed to yield the final result. The movies are acquired with a camera at average rates of 5 to 15 fps (frames per second) for durations ranging from a few dozen seconds to a few minutes; therefore, they can contain up to several thousand frames each.
Trouble is, all planets rotate about their axes: the trick is to stop the movie acquisition before the planet’s rotation kicks in and causes significant image blur. The maximum duration of a single movie can be figured out if all the imaging conditions are known well enough. This article is meant to discuss and explain a method to easily calculate the duration limit.
Main Limiting Factors
The maximum duration of a hi-res movie is affected by a number of factors. Here are the most important ones:
- The current target. Some planets, namely Jupiter, rotate very quickly;
- The planet’s apparent angular dimension;
- The imaging setup focal length;
- The physical specs of our sensor (size and number of pixels).
On the one hand, all these variables play a very important role; on the other hand, the type (i.e. optical configuration) of the telescope does not count that much. Of course, the final result will be greatly affected by the overall optical quality of our imaging rig.
Calculation Method
The calculation method is based upon very simple trigonometric rules. Let the figure below be our planet as viewed face-on from up above, so that it appears to rotate counterclockwise about its axis, which lies right in the geometric center of the circle.
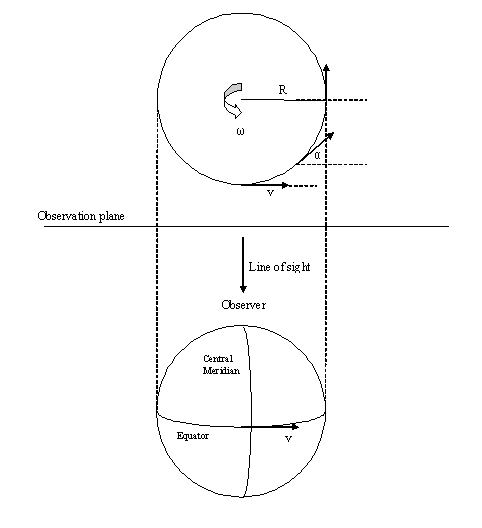
planet_engLet us call our planet’s apparent radius R (arcseconds)): it spins about its axis at an angular speed ?, which can be derived from the rotation period. The angular speed translates into a linear velocity v whose modulus is ?R. Since the planet’s disk projects onto the observation plane, only the component parallel to the latter has to be taken into account. This component has its peak in the center of the planet’s disk, and decreases towards the borders, where geometric distortion mars the visibility of the surface features.. With reference to the above figure, the velocity component along the observation plane can be derived as follows:
![]()
which reaches its maximum value for alpha = 0° and simplifies to v = ?R.
For small angles, the following formula holds:
![]()
where is the object’s apparent angular diameter (radians and arscseconds respectively), F is the telescope focal length and d is the linear dimension of the image projected onto the imaging sensor; F and d must be in the same units (typically mm). Here we can think of d as the maximum displacement allowable of the planet’s disk, before its rotation blurs our picture: if it amounts to no more than one single pixel, we won’t notice any blurring at all. For the sake of simplicity, let’s say our imaging sensor has square pixels, which is by the way the case with many popular cameras. The statement in italics can be mathematically written as follows:
![]()
which yields:
![]()
An Example
We now can give a practical example of how to apply our simple formula. Let us consider the following case:
- Mars, Jupiter and Saturn at opposition, i.e. at their largest and best. For Saturn, we take the diameter of the planet’s disk, not including its rings.
- The well known Sony ICX sensors found in the Philips webcams and many other cameras from Atik, Celestron, etc. These chips feature 5.6 micron-wide square pixels (5.6 microns = 0.0056 mm)
- 6-meter (6000 mm) focal length, which can be easily obtained by using a 3X barlow lens with an ubiquitous 8-inch SCT.
From the above formula the following table can be arranged:
| Planet | Radius (arcsec) | Rotation period | Omega (rad/s) | Delta T MAX (s) |
| Mars | 10.1 | 24h 37m | 7.09E-5 | 269 |
| Jupiter | 22.0 | 9h 50m | 1.77E-4 | 49 |
| Saturn | 10.3 | 10h 14m | 1.71E-4 | 109 |
The angular speed Omega is figured out by:
![]()
where T is the planet’s rotation period in seconds. For gaseous giants, we consider their equatorial system, which is also the fastest. The above table shows a maximum duration of about 4 minutes for Mars, 1 minute for Jupiter and 2 minutes for Saturn, but practical experience is somewhat different:
- The value for Mars sounds about right (from 3′ to 4′).
- On average, an one-minute Jupiter movie at 15 fps does not contain enough data. Therefore, we can push the limit up to 100-120 seconds so as to trade a slight (practically undetectable) blurring for much more information which will ultimately benefit the final image.
- A two-minute movie can be enough on Saturn, but since its surface details are less complex and feature-rich than on Jupiter, the three-minute limit can be easily exceeded.
Now the picture is quite clear: the only critical case is Jupiter, especially with tricolor imaging which calls for capturing three separate separate movies. Fortunately a 5.6-micron pixel with a 6000-mm flocal length means a 0.19-arcsecond resolution, which is way below the resolving power of most amateur astronomer equipment and the seeing of an average night. As a result, an 80-100% increase in the duration of movies is acceptable.
The other planets (Mercury, Venus, Uranus and Neptune) show hardly any surface detail, and are small enough so as not to pose any particular challenge. Anyway, the limit of 4 minutes is seldom exceeded for a number of practical reasons: movie size on the hard disk, flaws in the clock drive or drifting problems from inaccurate polar alignment, and so on. Tricolor imaging is even more complex, with waste of time for filter swapping and refocusing.
A Maximum Duration Calculator
The above calculations can be easily automatized for the lazy people who are interested only in the final result. An ad-hoc Microsoft Excel worksheet comes in really handy, and can be downloaded from this link.
This worksheet was developed and kindly provided by Marco Vedovato, fellow amateur astronomer and member of the Italian AstroHires planetary astronomy mailing list. It is presently available only in Italian, but an English version will follow shortly; in any case, its use is really straightforward. Here are a few directions:
- On loading, macros must be activated. If that isn’t enough for proper functioning, then the macro protection level must be decreased to “medium” or “low”.
- Choose the desired planet between Mars, Jupiter and Saturn. As was already explained, the other solar system objects can be disregarded.
- Choose the proper angular dimension range.
- Feed in the telescope equivalent focal length (in mm), which can be known a priori or even figured out by factoring in all the accessories in the optical train (e.g. barlow lenses, focal reducer, extension tubes, etc.).
- Feed in the sensor’s size of the pixel side, in microns. For Philips-like webcams, 5.60 is the correct value; for rectangular pixels, either the smaller side or an average value can be used.
As an alternative, the overall resolution (in arcseconds) permitted by the optical configuration and the metereological conditions can be used, if known.
The calculator outputs the estimated maximum length according to our model. The author can be contacted at antispam_vedovatom<at>virgilio.it (remove “antispam_”).
Refining the model
Our very model is clear and simple: however, it is based on quite a few simplifications. So, there is some room for improvement: in the following sections the most important approximations will be discussed, at least from a qualitative standpoint.
Center of the planet’s disk?
First off, talking about the planet disk center as the fastest-moving spot is an incorrect statement. Even though this does not affect the final result significantly, the fastest-moving region lies in the intersection of the planet’s equator with the central meridian. This area will be the same as the geometric center of the planet’s disk only if the rotation axis lies exactly on the observation plane and is therefore orthogonal to the line of sight. This does not apply if the axis inclination has a significant component along the line of sight, as is the case with Saturn and Mars.
Is the algorithm too strict?
Once again, it doesn’t hurt to point out that the method described in this article is most likely too strict, since it is based on the worst possible case, i.e. the planet’s intersection of the central meridian and equator. All other areas are more forgiving and can allow for longer acquisition times. Therefore, durations of up to twice as long as those given from the algorithm (or the Excel worksheet calculator) are still acceptable.
A more general formula
The maximum resolution attainable does not depend on the telescope used; out atmosphere plays a key role instead: the most important (and feared) bugaboo is undoubtedly the seeing. For example, if we know the current amostpheric condition and/or our optical equipment allows for a maximum resolution (called ?, arcseconds), we can generalize our inequality as follows:
![]()
The Excel worksheet also features the above formula in its bottom area. The overall resolution can be known a priori or can be figured out based on different qualitative and quantitative assumptions. According to the geometric approach, if we take:
![]()
we get the very same inequality shown earlier in this article.
Sampling and sensor noise
Nyquist/Shannon’s theorem states that a sampled band-limited analog signal can be reconstructed only if the sampling frequency is at least twice as big as the signal bandwidth. In 2-D imagery, this means the pixel size must not be bigger than half the size of the finest detail we want to make out. To put it in another way, the size of the smallest distinguishable detail is two pixels.
Nyquist’s criterion only holds for ideal conditions, where noise is absent or anyway negligible. However, single frames shot with uncooled sensors (as is the case with el-cheapo webcams) can be severely degraded by noise and have a very low signal-to-noise ratio. This problem can be partially overcome by stacking many frames together, but generally we’ll need more than two pixels. Therefore, oversampling by increasing the equivalent focal length will be of great help. The following link on the ESO website sheds some light on analog image sampling:
http://www.eso.org/projects/esomidas/doc/user/98NOV/volb/node12.html
Black-and-white and color sensors
The method described in this article only applies for black-and-white sensors, where each pixel samples the incoming signal and makes its very own contribution to form the final image. Color detectors, however, use the so-called “bayer matrix”, which consists of a grid whose elements are microlenses of one primary color (i.e. red, green, blue). The grid is superimposed to the pixel array: therefore, each pixel “sees” only one color out of three, while the other two are figured out by interpolation from the values of nearby pixels. This allows for inexpensive color imaging, but at the expense of resolution.
Of course, there is a way to shoot color images while taking advantage of the full sensor resolution: a black-and-white chip is used to image the target independently through three filters, one for each primary color (R, G, B). The three images can be made into one single color picture. While this method yields very good results, it does comes at a cost: more complex setup, filter swapping idle times, longer acquisition and processing, etc.
Conclusion
We know hi-res planetary imaging is affected by a host of different factors: nevertheless, pictures made by the most advanced amateurs clearly show that a solid technical background and hard work make it possible to get high-quality results of unquestionable esthetical and even scientific value. Of course, the most skilled amateurs will heavily rely on their personal experience rather than on the contents of this article. Moreover, the algorithm explained here leaves out a number of important factors, such as seeing, optical and mechanical limitations, etc.: but for rookies venturing into the wonderful world of hi-res planetary work, this article can be a good source of both theoretical explanation and useful numbers.
