This post is also available in: English (Inglese)
Come è noto, le stupende immagini planetarie ad alta risoluzione ottenute dagli astrofili di tutto il mondo tramite l’uso di telecamere e ottiche dei tipi più svariati si basano su un principio comune: la scelta e l’allineamento di una grande quantità di singoli fotogrammi a partire da un filmato che vengono poi sommati per ottenere l’immagine finale. I filmati, che possono contenere anche alcune migliaia di fotogrammi sono acquisiti mediamente tra i 5 e i 15 fotogrammi al secondo (frames per second, o fps); di conseguenza, ognuno di essi può potenzialmente durare anche diversi minuti.
Il problema è che tutti i pianeti ruotano: il segreto sta quindi nel contenere la durata dell’acquisizione in modo tale che la rotazione del pianeta non causi del mosso. Tale durata può essere opportunamente calcolata a priori se si conoscono tutte le condizioni di ripresa. In questo articolo si espone un metodo per effettuare tale calcolo.
Fattori limitanti principali
Numerosi sono i fattori che influenzano la durata massima di un filmato ad alta risoluzione prima che la rotazione del pianeta si faccia sentire. Essi sono:
- Il soggetto della ripresa. Alcuni pianeti, come ad esempio Giove, ruotano molto velocemente;
- Le dimensioni angolari del soggetto;
- La lunghezza focale del telescopio;
- Le caratteristiche geometriche del sensore, ed in particolare la dimensione dei pixel.
Tutte le variabili sopra esposte, come vedremo tra breve, giocano un ruolo determinante. In linea teorica, invece, poco (o addirittura affatto) conta il tipo di strumento utilizzato, i cui effetti semmai si ripercuotono sulla qualità globale dell’immagine.
Metodo di calcolo
Il metodo di calcolo si basa su banali considerazioni trigonometriche. Consideriamo la seguente immagine, raffigurante un ipotetico pianeta visto dall’alto:
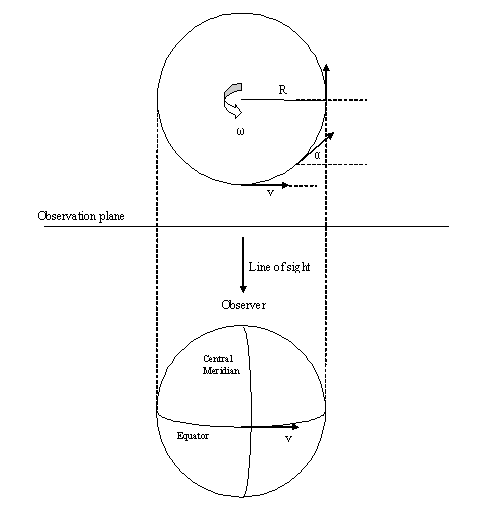
Tale pianeta, di raggio apparente R (misurato in secondi d’arco), ruoterà su se stesso con una velocità angolare ?, calcolabile direttamente dal suo periodo di rotazione. Tale velocità angolare si traduce ovviamente in una velocità geometrica tramite la ben nota formula v = ωR. Siccome l’immagine del pianeta è proiettata sul piano d’osservazione, risulta importante ai fini del movimento soltanto la componente ad esso parallela. Quindi, l’effetto sarà massimo al centro del disco del pianeta dove tale componente ha il valore più elevato, e minima verso i bordi dove la distorsione geometrica la rende addirittura trascurabile, alterando però di conseguenza anche la visibilità dei dettagli. Guardando la figura, la componente della velocità parallela al piano d’osservazione si calcola banalmente come segue:
![]()
che è massima quando l’angolo alfa è uguale a 0 e vale proprio v = ωR.
Ora, è noto che (per piccoli angoli):
![]()
ove θ è il diametro angolare apparente dell’oggetto (in radianti o secondi d’arco), F è la lunghezza focale dello strumento utilizzato e d è la dimensione dell’immagine dell’oggetto sul sensore di ripresa. F e d sono espressi nella stessa unità di misura, tipicamente mm. Nel nostro caso possiamo pensare a d come la quantità massima di cui l’immagine del pianeta si può spostare sul sensore prima che l’immagine sia alterata dalla rotazione: tale quantità corrisponde, idealmente, alla dimensione di un pixel del nostro sensore, soglia al di sotto della quale non siamo in grado di rilevare alcun spostamento. Per semplicità, supponiamo che il nostro sensore di ripresa abbia i pixel quadrati, cosa che per altro è abbastanza frequente. Abbiamo quindi che
![]()
da cui si perviene al risultato finale:
![]()
Nella quale DeltaT è la durata della ripresa del filmato, Dpixel la dimensione di un pixel del nostro sensore, e le altre grandezze sono quelle già menzionate nelle rispettive di unità di misura. Osserviamo che la quantità a secondo membro della disuguaglianza è evidentemente il valore massimo della durata della nostra ripresa.
Un esempio pratico
I semplici passaggi di cui sopra ci permettono ora di dare qualche esempio concreto. Consideriamo:
- Marte, Giove e Saturno all’opposizione, quando il diametro apparente è massimo. Per Saturno prendiamo il raggio del solo disco del pianeta, e non degli anelli.
- Sensori della Sony contenuti nelle webcam Philips (Vesta, ToUcam I e II) e in numerose altre telecamere (es. parecchie Atik, Celestron, ecc.) i cui pixel sono quadrati di 5.6 micron di lato (= 0.0056 mm).
- Focale di ripresa di 6 metri (6000 mm), ottenibile con un diffusissimo Schmidt-Cassegrain da 20 cm e Barlow 3X
Applicando la formula sopra esposta, possiamo stilare la seguente tabella:
| Pianeta | Raggio (arcsec) | Periodo di rotazione | Omega (rad/s) | Delta T MAX (s) |
| Mars | 10.1 | 24h 37m | 7.09E-5 | 269 |
| Jupiter | 22.0 | 9h 50m | 1.77E-4 | 49 |
| Saturn | 10.3 | 10h 14m | 1.71E-4 | 109 |
dove la velocità angolare ω è ottenuta tramite la ben nota formula:
![]()
dove T è il periodo di rotazione del pianeta in secondi; per i pianeti giganti si considera la rotazione del sistema equatoriale (il più veloce). Dalla tabella ricaviamo una durata di ripresa massima di circa 4 minuti per Marte, un minuto per Giove e circa due per Saturno.
Rispetto all’esperienza pratica troviamo che
- Il valore per Marte è in buon accordo (dai 3 ai 4′).
- Per Giove un filmato di un minuto a velocità tipicamente non superiori ai 15 fps non consente di raccogliere molta informazione. Normalmente, quindi, ci si può spingere fino a 100-120 secondi tollerando un lieve mosso, più che ampiamente compensato dal maggior numero di frame catturati.
- Per Saturno, un filmato da due minuti può già essere sufficiente. Tuttavia, dato che i particolari della superficie sono meno complessi e articolati di quelli di Giove, si possono raggiungere e superare i tre minuti.
Come si vede, l’unico pianeta davvero critico è Giove, soprattutto se si riprendono filmati separati in tricromia o quadricromia. Bisogna comunque considerare che un pixel di 5.6 micron equivale ad una risoluzione di 0.19 secondi d’arco con una focale di 6 metri, che è ben al di sotto di quanto consentito dal seeing e dall’apertura della maggior parte degli strumenti amatoriali; quindi, si può aumentare la lunghezza dei filmati anche dell’80-100%.
Gli altri pianeti del Sistema Solare (Mercurio, Venere, Urano, Nettuno) hanno superfici poco contrastate e/o un diametro abbastanza piccolo da non porre nessun problema. Nella pratica, raramente ci si spinge oltre i 4′ continuativi, indipendentemente dall’oggetto osservato, poiché intervengono altri fattori contrastanti di tipo diverso, quali ad esempio la dimensione del filmato, imprecisioni del moto orario che impediscono di tenere centrato il pianeta per tutto il tempo, ecc. Nel caso di acquisizione nei colori separati, dove c’è anche il problema dei tempi morti per il cambio del filtro ed eventuale rifocheggiatura, può essere utile sapere a priori queste informazioni.
Un calcolatore di durata massima
Il metodo sopra esposto, pur non essendo complicato, si presta piuttosto bene ad essere automatizzato a beneficio di coloro che fossero interessati al solo risultato finale. Il modo migliore per automatizzarlo è tramite un foglio Excel, scaricabile direttamente da questo indirizzo. Esso è stato sviluppato e gentilmente messo a disposizione da Marco Vedovato, collega astrofilo e membro della mailing list AstroHiRes. L’uso di questo foglio è estremamente semplice:
- All’apertura del foglio, le macro devono essere attivate premendo sull’apposito tasto (“Attiva Macro”). Se ciò non bastasse, abbassare il livello di protezione delle macro a “medio” o “basso”.
Scegliere il pianeta tra Marte, Giove e Saturno: per gli altri, come già detto, hanno poca importanza. - Scegliere l’intervallo di dimensione angolare apparente.
- Immettere la focale equivalente del sistema di ripresa, calcolata tenendo conto di tutti gli accessori presenti nel treno ottico (es. barlow, riduttori, prolunghe, ecc.).
- Immettere il lato (in micrometri) del sensore di ripresa. Ad esempio, 5.60 per le ben note webcam della Philps come nel caso discusso poco sopra.
- In alternativa, se si conosce la risoluzione complessiva permessa dalla serata (v. oltre), si può immettere quella
In output viene fornito il valore della durata massima consigliata. L’autore del foglio di calcolo può essere contattato al seguente indirizzo: antispam_vedovatom<at>virgilio.it (togliere antispam_).
Affinamenti ed estensioni
Il modello utilizzato fin qui è semplice e lineare, e risulta utile pertanto dal punto di vista didattico. Tuttavia, esso contiene alcune semplificazioni intrinseche, che in questo capitolo cerchiamo di superare almeno in parte.
Centro del disco del pianeta?
Un’affermazione non proprio corretta è innanzitutto quella che parla del centro del disco del pianeta come il punto che si sposta più velocemente. Anche se in realtà il risultato pratico non cambia, è doveroso precisare che il punto che si sposta più velocemente è quello corrispondente all’intersezione dell’ equatore e del meridiano centrale. Esso coinciderà col centro geometrico del disco se l’asse di rotazione è perpendicolare all’asse di vista (osservatore – pianeta); ciò non è più vero nel caso di pianeti la cui inclinazione abbia una componente significativa lungo l’asse di vista, come è ad esempio il caso di Marte e Saturno.
“Severità” del risultato
Non fa male ribadire ancora una volta che il procedimento usato è estremamente severo, perché esso tara il proprio limite sul caso peggiore, cioè lungo l’equatore del pianeta; tutte le altre zone reggono una durata maggiore. L’esperienza pratica accetta comunemente tempi anche doppi di quelli forniti dall’algoritmo (e dal relativo foglio di calcolo Excel).
Generalizzazione della formula
Molto spesso, la risoluzione massima raggiungibile è condizionata da fattori indipendenti dall’ottica utilizzata, e in generale introdotti dalla presenza dell’atmosfera: il più famoso (e odiato) di essi è il seeing. Se, ad esempio, sappiamo che la serata e/o anche il nostro sistema ottico nel suo complesso al massimo permette una risoluzione complessiva che chiamiamo ρ, espressa in secondi d’arco, possiamo generalizzare la disuguaglianza come segue:
![]()
Che è appunto il secondo caso contemplato dal foglio di calcolo Excel. Scegliendo uno dei criteri possibili con cui la risoluzione può essere determinata, in particolare ponendo:
![]()
si ricava la formula esposta all’inizio di questo articolo.
Campionamento e rumore del sensore
Il criterio di Nyquist/Shannon stabilisce che un segnale analogico campionato (di banda limitata in frequenza) può essere ricostruito solo se la frequenza di campionamento è il doppio della banda massima. Nel campo delle immagini, ciò si traduce in pratica nel fatto che la dimensione del minimo elemento del sensore (pixel) dev’essere al massimo la metà del più piccolo particolare che si vuole distinguere. In altre parole, si può dire che la dimensione minima del più piccolo particolare sicuramente distinguibile è di due pixel.
Il criterio di Nyquist così, tuttavia, vale soltanto condizioni ideali, in cui il rumore sia assente o addirittura trascurabile. Purtroppo, però, i singoli fotogrammi ripresi con sensori non raffreddati (come quelli delle webcam) sono pesantemente degradati dal rumore (basso rapporto segnale/rumore). Questo problema può essere in parte risolto tramite la somma di molti singoli fotogrammi, ma in generale saranno necessari più di due pixel; pertanto, converrà sovracampionare aumentando di consegunza la lunghezza focale di ripresa. Il seguente link sul sito dell’ESO (in inglese) contiene una breve ma molto chiara spiegazione del campionamento delle immagini analogiche e delle relative problematiche:
http://www.eso.org/projects/esomidas/doc/user/98NOV/volb/node12.html
Sensori a colori e in bianco e nero
Il metodo esposto a rigore è applicabile soltanto a sensori in bianco e nero, nei quali ogni pixel campiona il segnale e contribuisce a formare l’immagine. Nei sensori a colori, invece, troviamo la cosiddetta matrice di bayer: si tratta di una griglia di microlenti dei tre colori fondamentali (rosso, verde, blu) ognuna delle quali è sovrapposta a un pixel. La conseguenza di ciò è che ogni pixel campiona un solo colore, mentre i valori degli altri due colori per quel pixel vengono calcolati per interpolazione a partire dai pixel adiacenti. Ciò, evidentemente, peggiora la risoluzione effettiva del nostro sistema.
Il modo per ovviare a questo inconveniente esiste, anche se chiaramente è più oneroso. Esso consiste nell’utilizzare un sensore in bianco e nero e riprendere tre filmati distinti attraverso altrettanti filtri (uno per ciascun colore primario), sommando alla fine i tre canali in una unica immagine.
Conclusioni
Come abbiamo visto, i risultati nel campo della ripresa planetaria ad alta risoluzione dipendono da una miriade di fattori diversi: ciononostante, le immagini ottenute dai dilettanti più esperti dimostrano che è possibile, la costanza e solide basi tecniche, risultati significativi da un punto di vista scientifico. Ovviamente, l’astrofilo esperto si fiderà più della propria esperienza anche in considerazione di altri fattori contingenti di cui qui non si è tenuto conto, come ad esempio il seeing, i limiti impostri dalla propria strumentazione, ecc. e quindi non avrà certamente bisogno di farsi i conti ogni volta. Ma per il principiante appena accostatosi alle tecniche di ripresa planetaria, le informazioni contenute in questo articolo possono costituire una buona fonte per capire le motivazioni di certe scelte pratiche.
